INDUCTIVE CUBIC NETWORKS OF

JOSEPHSON JUNCTIONS

Roberto De Luca

INFM - DIIMA - Università degli Studi di Salerno

I-84084 Fisciano (SA) - ITALY

The electrodynamic properties of cubic networks of Josephson junctions are studied by means of a combined analytic and numerical procedure. The full inductance matrix for the system is taken into account and the dynamical equations for the phase differences across the junctions are written in a compact matrix form. The general properties of the resulting non-linear coupled differential equations are analyzed.

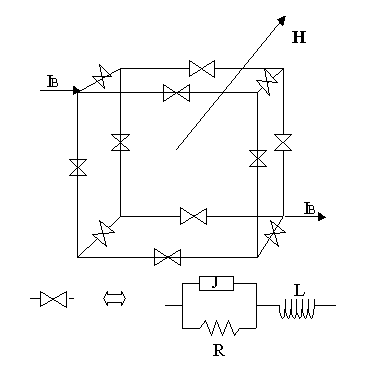
In order to study the electrodynamic properties of the model shown in Fig.1, we develop a novel analytic approach, by which we are able to write the dynamical equations of the gauge invariant superconducting phase differences across the junctions in vectorial form.

FIG.1 The inductive cubic network of Josephson junctions.

Dynamical equation for the superconducting phase differences

D_J(j)+I_J sinj=I (1)

where the vector j is taken as follows:

j=(j_x(0),j_x(ay),j_x(az),j_x(ay+az),

j_y(0),j_y(ax),j_y(az),j_y(ax+az),

j_z(0),j_z(ax),j_z(ay),j_z(ax+ ay)) ,

and where D_J is the following linear operator [1]:

O_J(*)=(F₀/2pR)d/dt(*^. ).

The symbolic notation of Eq.(1) assigns a precise meaning to the sine term. Indeed, sinj is to be though as the vector whose components are the quantities sinj_x . Finally, the twelve components of the vector I are the branch currents in the cubic system.

Fluxoid quantization for elementary loops [1]

(2p /F₀)F = Fj +2p n (2)

where F is the flux vector with only five components, given the null divergence of magnetic induction, F is a 5x12 matrix with elements 0, +1,-1, and n is a vector with five integral components.

Classical Electrodynamics

Loop-currents vs. branch currents

I = -FI (3)

where the loop current vector I has five components I_mn (r) , r being the position of the loop in space.

Flux-current relations

F=f_ext G+MI (4)

where f_ext =m₀Ha², H being the amplitude of the applied magnetic field, G is the five-component vector defining the direction in which the file is applied and M is the mutual inductance matrix [2].

Kirchhoff’s law of currents

I=TJ-I_B (5)

where T is a 12x5 matrix with elements 0, +1,-1, J is a vector having as components five independent branch currents and I_B is the bias-current vector with twelve components.

By combining the above equations we can write the dynamical equations for the superconducting phase differences as follows:

dj/dt+sinj+(1/2pb)Aj=f (6)

where A=LT(FT)^-1G^-1F , L being the self-inductance coefficient relative to a single branch of the network, and f is the forcing term containing information on the field amplitude, on the field direction, on the bias current intensity and on the initial magnetic state of the system. In Eq. (6) b=LI_J/F₀ and t=2pRI_Jt/F₀ .

The above set of non-linear first-order ordinary differential equations is seen to be formally identical to that obtained for a d.c. SQUID when the same matrix approach is used for the latter. Therefore, the same type of concepts, which apply to d.c. SQUID's, may be adopted in this more complex case.

Periodicity of the branch voltages with respect to time

It can be proven that, when the junctions are in the running state, the voltage across the branch containing the junction shows periodicity with respect to time.

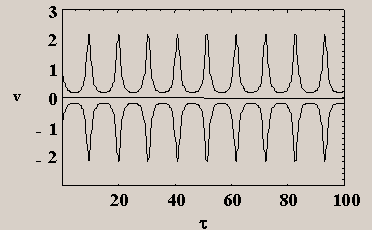
In Fig. 2 we show the voltages across all the branches in the network for b=0.1 and for f_ex=0.

FIG.2 Branch voltages for b=0.1 and for f_ex=0. The bias current is 3.5 I_J, so that some JJ’s are in the running state, some still in the zero-voltage state.

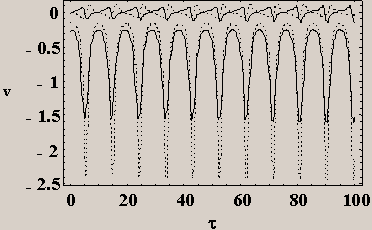In Fig. 3a, 3b, 3c we show the voltages across the branches lying in the x, y, and z direction, respectively, for b=0.1 and for f_ex=0.2.

FIG.3a Voltages across branches lying in the x direction for b=0.1 and for f_ex=0.2. The bias current is 3.5I_J. The upper curves are for JJ’s on the branches at position r=0 (full line) and at r=ay+az (dashed line), while the lower curves are for JJ’s on the branches at position r=ay (dashed line) and at r=az (full line).

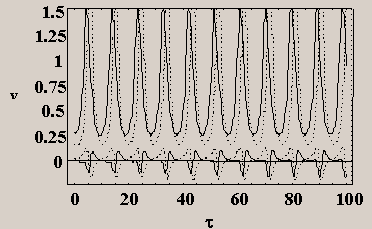
FIG.3b Voltages across branches lying in the y direction for b=0.1 and for f_ex=0.2. The bias current is 3.5I_J. The upper curves are for JJ’s on the branches at position r=ax+az (dashed line) and at r=0 (full line), while the lower curves are for JJ’s on the branches at position r=ax (dashed line) and at r=az (full line).

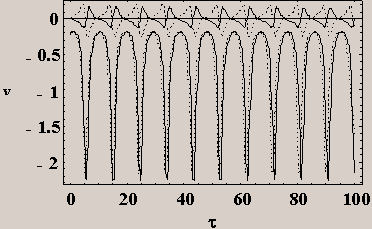
FIG.3c Voltages across branches lying in the z direction for b=0.1 and for f_ex=0.2. The bias current is 3.5I_J. The upper curves are for JJ’s on the branches at position r=0 (dashed line) and at r=ax+ay (full line), while the lower curves are for JJ’s on the branches at position r=ax (dashed line) and at r=ay (full line).

Periodicity of the observable voltages with respect to the applied flux

It can be also proven that the time-averaged voltage across the branches are periodic with respect to the applied flux number Y_ex=F_ex /F₀ (with period DY_ex)if the magnetic field is oriented along a direction h=(cosg_x,cosg_y,cosg_z) satisfying the following relations:

cosg_x DY_ex = i ; cosg_y DY_ex = j; cosg_z DY_ex = k , where i, j, k are integers, so that the period can be found to be DY_ex = ( i²+j² +k²)^1/2 .

It is possible to make a systematic study of the periodicity of the observable voltages with respect to the applied flux number. Here we give only an example of how it can be detected numerically.

Take, for example, the field applied along the z axis. Then i=j=0 and k=1, so that DY_ex = 1.

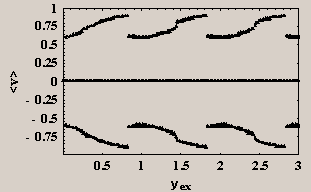
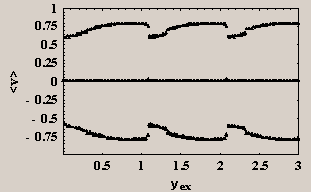
FIG.4 left/right Average voltages across all the branches in the network when the magnetic field is applied along the z direction. Hereb=0.1 (left) and b=0.2 (right) and the bias current is 3.5I_J.

Take, as another example, the field applied at 45° with respect to the z axis in the y-z plane. Then i=0 and j=k=1, so that DY_ex = 2^1/2.

FIG.5 Average voltages across all the branches in the network when the magnetic field is applied along the (0,1,1) direction. Hereb=0.1 and the bias current is 3.5I_J.

Again, we can consider the field applied along the cube diagonal. Then i=j=k=1, so that

DY_ex = 3^1/2.

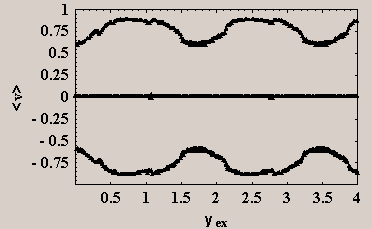
FIG.6 Average voltages across all the branches in the network when the magnetic field is applied along the (1,1,1) direction. Hereb=0.1 and the bias current is 3.5I_J.

REFERENCES

[1] A. Barone and G. Paternò, Physics and applications of the Josephson effect (Wiley, New York, 1982).

[2] R. De Luca, T. Di Matteo, A. Tuohimaa and J. Paasi, Phys. Rev. B 57, 1173 (1998).