
|
SICUREZZA NELL'INDUSTRIA DI PROCESSO
Fondamenti |

|
SICUREZZA NELL'INDUSTRIA DI PROCESSO
Fondamenti |
| HOME |
| ELEMENTI INTRODUTTIVI |
| CASI STORICI |
| SCHEDE DI SICUREZZA |
| ANALISI DI RISCHIO |
| GLOSSARIO |
| LEGGI E REGOLAMENTI |
| PUBBLICAZIONI |
| LINK |
| Efflusso di gas/vapori |
Il principio di conservazione dell’energia, applicato a processi adiabatici e isoentropici di gas/vapori assunti come fluidi perfetti e per i quali le forze di massa sono trascurabili, si riduce a :
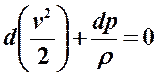
v la velocità, p la pressione e ρ la densità. Il secondo termine corrisponde alla variazione di entalpia (dε) per cui : 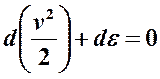
essendo: 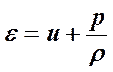
ove u è l’energia interna. In definitiva : 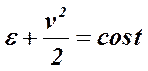
ovvero un gas in uscita da un orifizio acquista energia cinetica a spese dell’entalpia nelle condizioni a monte del flusso. Nel caso di un gas perfetto è: 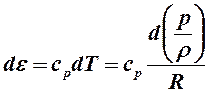
essendo T la temperatura, cp il calore specifico a pressione costante e R la costante universale dei gas che si può esprimere in funzione dei calori specifici a pressione e a volume costante (cv): 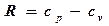
Integrando si ricava 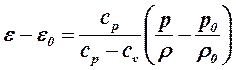
ove i parametri con indice o si riferiscono alle condizioni a monte della sezione di efflusso. Poiché : 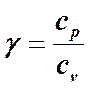
Si ricava che : 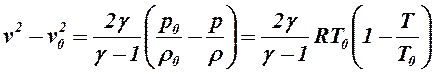
Per risolvere il problema resta da conoscere il legame tra pressione e densità che in condizioni adiabatiche, come quelle ipotizzate che sono verosimili per efflussi di gas in pressione, è dato dall’equazione di Poisson: 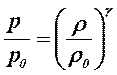
per cui la velocità di efflusso può esplicitarsi in funzione delle condizioni a monte della sezione di efflusso: 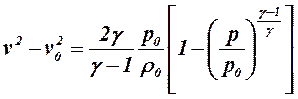
o delle condizioni a valle : 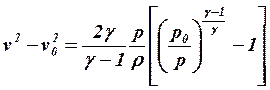
Nota la velocità e la sezione (ω) della vena di un fluido di densità nota si può calcolare la portata massica : 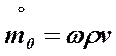
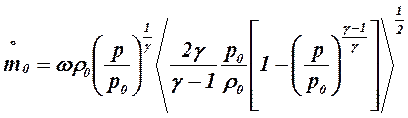
Si noti che nel caso di un efflusso di gas/vapore da un foro sulla parete di un recipiente la vena fluida la vena fluida si contrae sino ad un massimo per poi riaprirsi. ω è la sezione minima contratta (incognita) a valle del foro per cui per applicare più correttamente la precedente equazione si assume un rapporto lineare tra le due grandezze A x CD = ω, ove CD è un coefficiente correttivo di contrazione. Tornando alla precedente equazione della portata massica, si osserva che essa ha una doppia dipendenza, diretta e inversa, dal rapporto p/po. In particolare, quando la pressione interna è uguale a quella esterna essa si annulla: 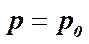
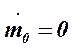
mentre all’aumentare del rapporto tra pressione a monte e a valle la portata cresce rapidamente sino ad un valore massimo : 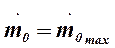
che si ricava derivando la relazione rispetto al rapporto p/po. Questa condizione si verifica in corrispondenza di un valore di pressione detta critica (o sonica) : 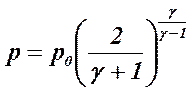
Per la maggior parte dei gas γ è compreso tra 1,1 e 1,67 (gas monoatomici) per cui il rapporto tra la pressione critica e quella a monte varia tra: 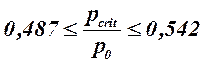
In corrispondenza della condizione critica la velocità critica (sonica) di efflusso è : 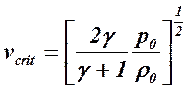
la quale, come si osserva, dipende solo dalle condizioni a monte. A sua volta la portata in condizioni critiche è data da : 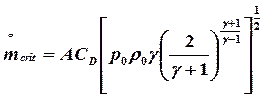
Mentre nelle situazioni subcritiche per cui : 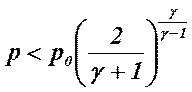
La portata massica si può sempre rapportare a quella critica riscrivendo la relazione generale come: 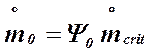
ove il termine Ψo è uguale a : 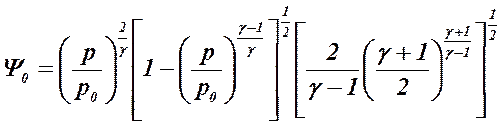
In definitiva la portata massica assume la forma generale : 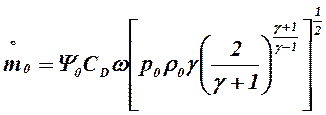
|