Copyright © A.Di Egidio
Dynamics
The behaviour of a cable-satellite system in several internal resonance condition has been analyzed and the resonant dynamics
studied in detail.
In the field of the sensitivity analysis of the spectral proprierties of linear systems, a general procedure that make possible to
analyze the eigenvalues and the eigenvectors sensitivity of conservative systems, also in the case of multiple eigenvalues,
has been developed.
Refering to the use of the Multiple Scale Method for the study of the dynamics of resonant systems, a procedure able to identify the
standard form of the modulation equations with the aim to make possible the study of the steady-state solutions and of their stability,
has been developed.
The structure of the modulation equations has been also studied in deep. Some algorithms and theorems able to to furnish, only
by the knowledge of the resonant conditions, the formal structure of the equations, the classes of motion admitted by the system
and other informations regarding the stability of these solutions, have been proposed. An analytical and a graphical approach have
been developed to reach the goal.
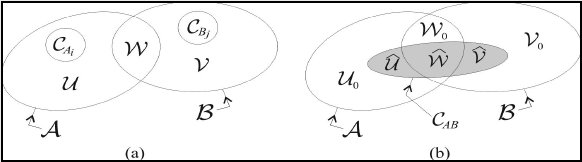
Fig. 1.2: Graphical interaction between two families of elementary classes of motion
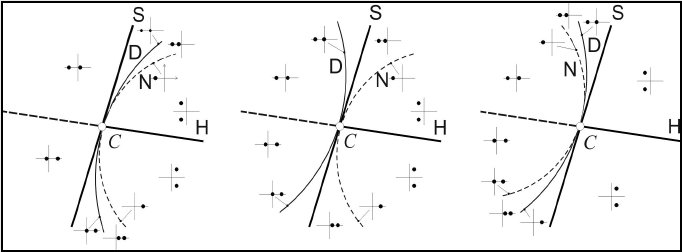
Fig. 1.1: Stability diagram in the generic case: refined analysis
UNIVERSITY OF L'AQUILA - ITALY
Dynamics
D.I.C.E.A.A. - Dipartimento di Ingegneria Civile, Edile-Architettura e Ambientale