Shell

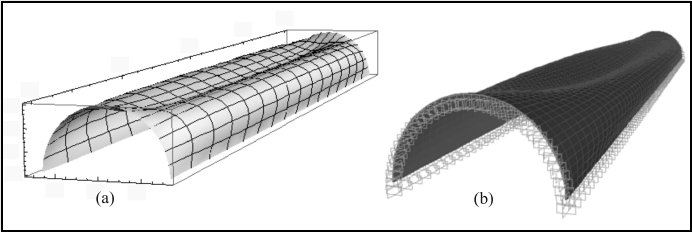
Fig. 8.1: Deformation of entirely clamped barrel shell: (a) Semi-analytical solution; (b) FE solution

A model of linear, internally constrained shell with single, constant curvature,is used to describe the behaviour of existing structures, such as barrel shells. A linear, elastic, isotropic material is considered. Observing that in the shell two families of mono-dimensional interacting beams can be recognised: straight longitudinal beams and transversal arches, non-conventional semi-analytical approximate solution, which uses the method of separation of variables, is proposed. By using an integral procedure, reduced differential, ordinary equations, capable of describing the behaviour of the shell, are obtained. Both linear static behaviour and longitudinal buckling of the shell are investigated. The approximate solution proposed leads to results which match those of a finite element model and permits to give a descripion of shells similar to that of beams on elastic soil. With regard to the linear static behaviour of the shell, a short, and a long, characterization is proposed and original graphical abaci are obtained with the purpose of facilitating the classification. An extensive study is then performed in order to analyse the buckling of the shells.

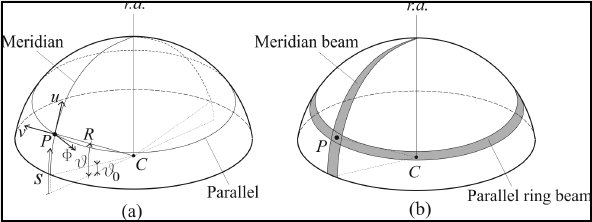
In spherical shells, due to the axial-symmetry of the system, all the quantities involved in the elastic problem only depend on the curvilinear abscissa along the meridian lines. Hence, the mathematical domain of the model becomes mono-dimensional. However, in the classical model of axial-symmetric spherical shells, the kinematic problem is not the adjoint of the static problem. With the aim to clarify this aspect, a mono-dimensional linear model of axial-symmetric spherical shells has been proposed. The adopted mono-dimensional approach furnishes a model where the kinematic problem is the adjoint of the static problem. This model, able to describe the linear static behaviour of the shell, can be considered as a curved beam posed on an elastic variable soil. The comparison among approximate analytical models and a Finite Element one confirm the effectiveness of the proposed mono-dimensional approach. Graphical abaci, that permit a handy classification, are then proposed, depending only on the geometrical characteristics of the shell.

Fig. 8.2: Spherical shell

D.I.C.E.A.A. - Dipartimento di Ingegneria Civile, Edile-Architettura e Ambientale

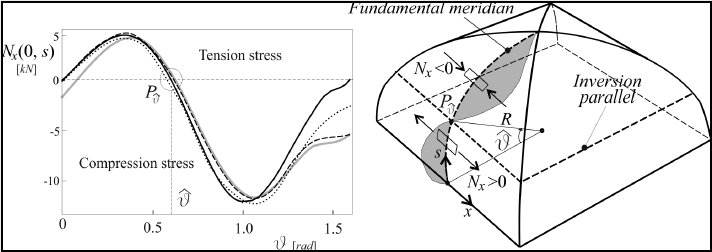
A semi-analytical approach is followed in order to obtain an approximate solution for an analytical model describing the static behaviour of pavilion shells. With the aim to parametrically investigate the distribution of the linear elastic tensile stresses, a linear elastic isotropic behaviour of the material is considered. Inside the pavilion shell, a family of arches and a family of straight beams can be recognized. This assumption justifies the separation of the variables which is at the basis of the proposed semi-analytical approach. The sensitivity of the behaviour of the shells to the values of the mechanical and geometrical parameters characterizing the system is investigated. Comparisons with results obtained by finite element models are performed to confirm both the validity of the semi-analytical approach and the provided results. Since only a linear elastic isotropic material has been taken into account, the results do not claim to describe the behaviour of masonry pavilion vaults.

Fig. 8.3: Tensile stresses in a pavilion shell