Copyright © A.Di Egidio
Bifurcation and Stability
In the field of the stability of elastic discrete systems, by focusing the attention to phenomena exibiting bifurcation with codimension
greater than one, an unitary procedure based on the Multiple Scale Method, able to study both defective and non-defective bifurcations
of mechanical systems under non-conservative loads, has been developed. The critical and post-critical behaviour of multiple zero
and Hopf bifurcations, double Hofp bifurcations in several internal resonance conditions, have been studied in deep.

The method based on the Multiple Scale Method to study the bifurcations with high codimension of discrete systems has been extended
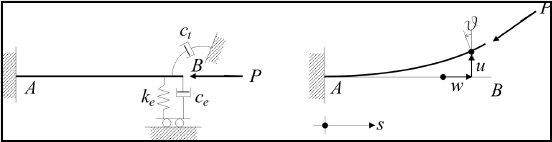
to continuous systems. A simple mechanical system exibiting a very rich critical scenario has been analyzed. Thi system is constituted
by a planar cantilever beam properly constrained and loaded by a follower force. The critical and post-critical behaviour of static
and Hopf bifurcations, double divergence, non-resonat Hopf and Hopf-divergence bifurcation have been analyzed.
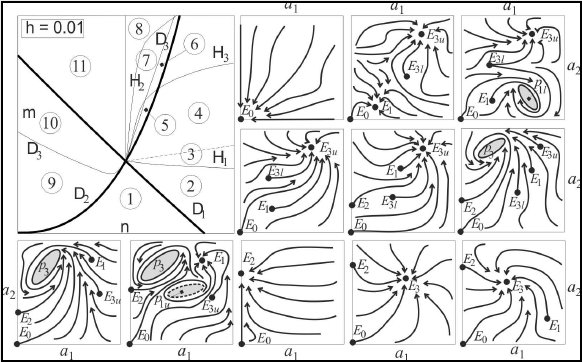
Fig. 3.1: Phase-portrait scenario for the double Hopf with 1:2 internal resonance condition
UNIVERSITY OF L'AQUILA - ITALY
Bifurcation, Stability
A particular classical mechanical system constituted by a 3D cantilever beam loaded at the free-end section by a tangetial torsional
moment and by a dead axial force is studied. When the study of the flexural-torsional instability is performed, the system exibits the
so called 'paradox of Nicolai'. The study aims to understand in deep the reasons for wich the paradox manifest itself.
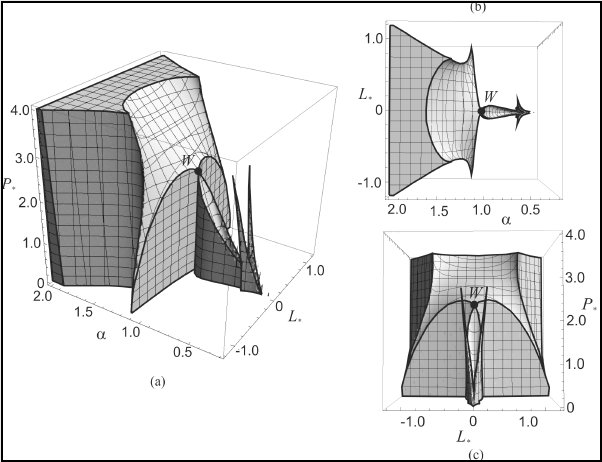
Fig. 3.3: Stability region for the elliptic cross-section of the rod
D.I.C.E.A.A. - Dipartimento di Ingegneria Civile, Edile-Architettura e Ambientale