Copyright © A.Di Egidio
UNIVERSITY OF L'AQUILA - ITALY
D.I.C.E.A.A. - Dipartimento di Ingegneria Civile, Edile-Architettura e Ambientale
Rigid block
Rigid Block
Passive Control
The effects of a mass damper on the rocking motion of a non-symmetric rigid block, subject to one-sine pulse type excitation, has
been investigated. The damper is modelled as a pendulum, hinged at the top of the block, with the mass lumped at the end. The
equations of rocking motion, the uplift and the impact conditions heve been derived and the results have been obtained
by numerical integration of these equations. An extensive parametric analysis has been performed with the objective
to understand if it is possible to find the optimal properties of the pendulum, capable to make more difficult the overturning of
the body. The results show that the presence of the mass damper, if correctly designed, leads to a general improvement of the response
of the system, since the overturning of the block occurs for values, of the amplitude of the base excitation, higher than those
observed where no mass damper is used.
Fig. 6.2: Block with the pendulum mass damper


The effects of a mass damper on the rocking motion of a non-symmetric rigid-block-like structure, subject to different seismic excitation,
are investigated. The damper is modelled as a single degree of freedom oscillating mass, running at the top of the block and connected
to it by a linear visco-elastic device. The equations of rocking motion, the uplift and the impact conditions are derived. A non-dimensionalization
of the governing equations is performed with the aim to obtain an extensive parametric analysis. The slenderness and the base
of the rigid block, the eccentricity of the center of mass are taken as variable parameters in the analyses. The main objective of
the study is to check the performance of the damper versus the spectral characteristics of the seismic input. Three earthquake registrations
with different frequency contents are used in the analyses. The results show that the presence of the mass damper leads to different
levels of improvement of the response of the system, depending on the spectral characteristics of the seismic input. Curves providing
the overturning slenderness of blocks of specific sizes versus the characteristics of the TMD are obtained.


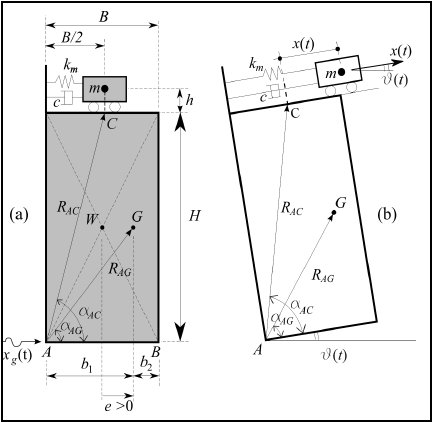
Fig. 6.3: Block with the oscillating mass damper
In this paper the effectiveness of a mass-damper dynamic absorber in preventing rigid blocks from overturning is investigated. The
mass-damper is modelled as a pendulum, hinged at the top of the block, with the mass lumped at the end. Under an impulsive one-sine
base excitation, an extensive parametric analysis is performed. In particular the frequency, the amplitude of the excitation along
with the block and the mass damper's geometrical characteristics have been taken as variable parameters. Overturning spectra,
providing the excitation amplitude of block's overturning versus the frequency of the one-sine pulse, are obtained. An experimental
test is performed by using a linear electromagnetic motor that is used to realize a small mono-dimensional shaking table. A rigid
block with fixed geometrical characteristics equipped with a pendulum is tested. Under a one-sine and a one-cosine impulsive base
excitations, the overturning spectra are obtained. The results show that the presence of the mass damper leads to a general improvement
of the dynamic response of the system.


Fig. 6.4: Experimental setup
A. Di Egidio, R. Alaggio, A. Aloisio, A.M. de Leo, A. Contento, M. Tursini, ‘Analytical and experimental investigation into the effectiveness of a pendulum dynamic absorber to protect rigid blocks from overturning’, Int. Journal of NonLinear Mechanics, Vol. 115, pp. 1-10, 2019.
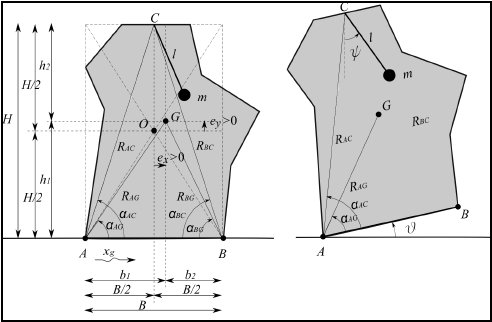
The protection of non-structural elements is having an increasing interest in the scientific literature. Many non-structural elements
undergo to a rocking motion when they are subjected to base excitation. For instance, cabinets and racks for both civil and industrial
use fall into this class. This paper aims to improve the dynamic and seismic behaviour of a rocking body under base excitation by
reducing the amplitude of the rocking motion and consequently reducing the likelihood of their overturning. To achieve such objective,
the body is modelled as an assembly of rigid parts connected with deformable devices that allow the body to change its geometrical
configuration during the motion. Although the model presented in this paper is derived for a specific configuration of the body, such
model can be easily generalized to describe similar non-structural elements. The improvement of the behaviour of the body due to its
ability to deform is assessed with an extensive parametric analysis that is performed considering both one-sine pulse and seismic
excitation. The results show that the deformation of the assembly that occurs before and after the start of the rocking motion improves
the performances of the body.


Fig. 6.5: Deformable rcking body

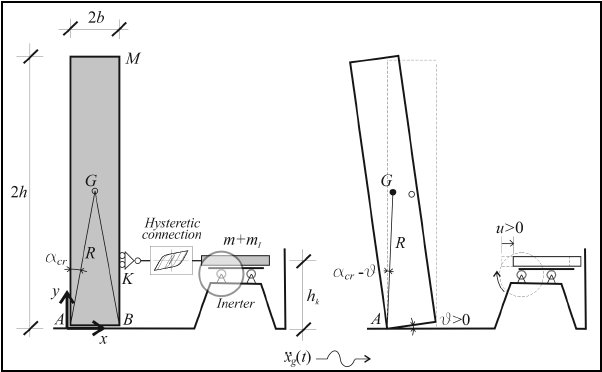
The protection of rigid block-like structures against the seismic hazard is a widely studied topic and has been achieved to different
degrees with active and passive protection methods. For the protection of rigid block-like structures, this paper proposes the coupling
of a rigid block-like structure, modelled as a single rigid block, with an external, auxiliary system through a hysteretic elasto-plastic
device. The auxiliary system is constituted by an oscillating mass, whose inertial effects are amplified by the use of an inerter
device. The auxiliary system works as a hysteretic mass damper. The elasto-plastic behaviour of the coupling device is described by
the Bouc-Wen model. The mechanical model of the coupled system has two degrees of freedom, and its equations of motion can be written
by following a direct approach. A preliminary analysis is performed by exciting different coupled systems and the corresponding stand-alone
rigid blocks with harmonic base accelerations. Such an investigation is aimed at understanding the sensitivity of the dynamics of
the coupled systems to the characteristics of the rigid blocks and auxiliary systems and is performed by comparing the frequency-response
curves of the coupled systems with those of the corresponding stand-alone rigid blocks. A further analysis is performed to verify
the effectiveness of the proposed protection methodology under seismic excitation. Both the harmonic and seismic analyses show that
the main parameter to be tuned to achieve the protection of the rigid block-like structures is the apparent mass of the inerter device.
A proper choice of such a mass improves the dynamics of the rigid block-like structures leading to smaller oscillations for the same
level of excitation.


Fig. 6.6: Deformable rcking body