active

D.I.C.E.A.A. - Dipartimento di Ingegneria Civile, Edile-Architettura e Ambientale

In recent years only a very small number of studies analysed the use of active or semi-active control methods in order to avoid the overturning of rigid block-like structures under base excitation. In this paper, an active control algorithm, based on the pole placement method, is developed for rigid blocks starting from a description of the the rocking motion through linearised equations. Such an approach is \textcolor{red}{an excellent approximation} for slender rigid blocks for which linearised equations can fully describe the rocking motion due to the smallness of the inclination angle. The control method has two objective: the first one is related to the possibility of vanishing the external excitation at each instant, the second one is to make the rest position of the block a stable point. The first analyses revealed the good robustness of the control algorithm to a variation of the sampling time and of the time-delay of the real control devices. Furthermore, the further parametric analyses pointed out the good effectiveness of the proposed control algorithm both in the reduction of the rocking angle and in the protection from the overturning, also in the case of \textcolor{red}{blocks with low slenderness}. Overturning spectra are obtained in the case of rigid block with and without active control.

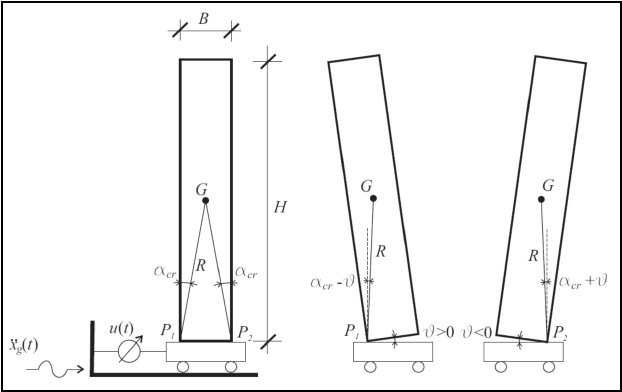
Fig. 7.1: Controlled rigid block

In recent years, several studies proposed new techniques aimed at improving the performances of rigid block-like objects under base excitation. The majority of these studies considered passive control methods, such as base isolation or other techniques based on the tuned mass damper principle. Only few studies considered active and semi-active control methods applied to the dynamics of rigid blocks. This paper proposes an active control method for symmetric rigid blocks that is based on the Linear Quadratic Regulator approach. The optimal control law is obtained starting from the linearized equation of motion. The effectiveness of the proposed control method is investigated comparing the behaviour of rigid blocks with and without active control under harmonic and seismic excitation. The results are summarized in overturning spectra, in the case of harmonic excitation, and rocking maps, in the case of seismic excitation. Although the proposed active control method is expected to work well for slender blocks, specific analyses show that the method also improves the dynamics of no-slender blocks and is effective for blocks with different geometrical characteristics. Moreover, the results show that the control law has a good robustness with respect to the sampling time and the time-delay.

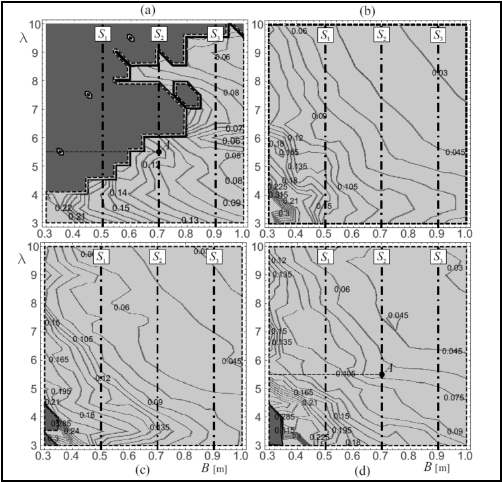
Fig. 7.2: Rocking maps under Parkfield earthquake: (a) Without active control; (b-c-d) with active control and different time-delays.

Several researchers proposed innovative techniques for the improvement of the dynamic and seismic performances of rigid block-like elements. These techniques were mostly based on passive control methods, such as base isolation or the use of tuned mass dampers and dynamic mass absorbers. Only a few researchers studied active control methods applied to the dynamics of rigid blocks. This paper proposes an active control method for rigid block-like elements based on the Pole Placement Method algorithm, which is used to drive a mass running on the top of the rigid block-like elements. The optimal control law obtained with the Pole Placement Method is obtained starting from the linearised equation of motion. The effectiveness of the proposed control method is investigated comparing the behaviour of rigid block-like elements with and without active control under harmonic and seismic excitation. The results are summarised in overturning spectra, in the case of harmonic excitation, and rocking maps, in the case of seismic excitation. Preliminary analyses show that the control law has good robustness with respect to the time-delays and a unique setting of the control coefficient is able to provide good performances in wide ranges of the geometrical characteristics of the rigid block-like element. Finally, results show the effectiveness of the proposed active control method for both harmonic and seismic excitations.

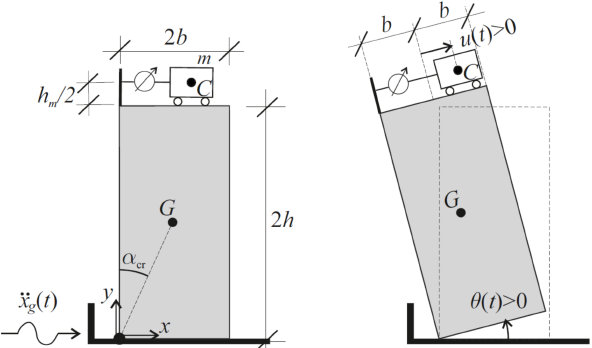
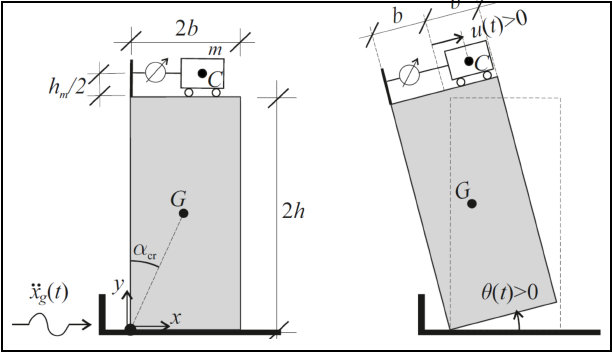
Fig. 7.3: Rigid block: Geometrical characterisation; positive directions of the control displacement ?? and rocking angle ??.